中学3年生の狸雄は、高校受験の勉強をサボって町中をブラブラ散歩していました。そんな狸雄に色黒の老人が話しかけてきました。老人は「知玄(ちげん)」と名乗り、「少年よ、わしと囲碁を打たんかの?」と誘ってきます。

おいら、囲碁のルールを知りません。
狸雄が誘いを断ると、知玄は「囲碁のルールを知らんとは嘆かわしい! それなら、この問題を解け! 解けねば、呪われるぞ!」と一方的に問題を突き付けてきました。

迷惑なじいさんだなあ。でも、呪われるのは嫌だから、問題を解くか……。
狸雄と一緒に、中学受験算数でおなじみの方陣算を解きましょう。方陣算は高校入試でも出題されることがあるので、苦手な高校受験生もチャレンジしてみてください。
方陣算はどんな特殊算なの?
【問題1】下の図のように、黒い碁石を並べて正方形を作ります。
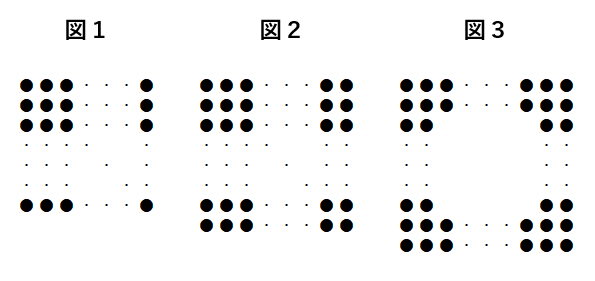
(1) 図1のように、碁石をしきつめて正方形を作ったら、碁石が20個あまりました。そこで、図2のように、正方形の一辺に並ぶ碁石を1個増やして新しい正方形を作ろうとしたら、碁石が7個足りませんでした。碁石は全部で何個ですか。
(2) (1)の碁石を2周させて図3のような正方形を作ります。碁石を最も多く並べるとき、正方形の一辺に並ぶ碁石は何個ですか。また、あまった碁石は何個ですか。
碁石を並べて正方形を作るとき、その碁石の数を求める特殊算が「方陣算」です。「方陣」は正方形を意味しますが、長方形や三角形などを作る問題も方陣算に含まれます。
また、図1や図2のように、正方形の内部まで碁石をぎっしりしきつめている場合を「中実方陣」といいます。一方、図3のように、正方形の内部に碁石を並べない場合を「中空方陣」といいます。
中実方陣の場合、正方形の一辺に並ぶ碁石をn個とすると、正方形を作る碁石は全部でn×n個です。一方、中空方陣の場合、碁石の数を求めるのに工夫が必要です。

おいらは中学生だから、方程式で問題を解くよ!
中実方陣で碁石の数を求めるには?
(1)は中実方陣の問題です。中実方陣で碁石の数を求める場合、まずは正方形の一辺に並ぶ碁石の数を求めましょう。
図1の正方形から図2の正方形を作るとき、増える碁石は、図1であまった碁石20個と、図2で不足した碁石7個の和なので20+7=27(個)です。(27-1)÷2=13(個)が、図1の正方形の一辺に並ぶ碁石の数です。したがって、(1)の答えは13×13+20=189(個)です。(説明がわかりにくければ、下の図を参考にしてください)
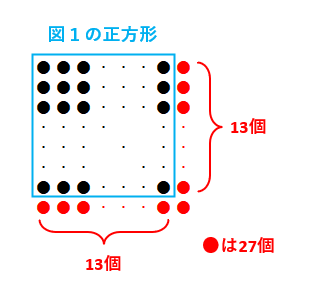

図1の正方形の一辺に並ぶ碁石をn個とすると、正方形を作る碁石の数はn2個だよ。だから、碁石は全部で(n2+20)個なんだ。
一方、図2の正方形の一辺に並ぶ碁石は(n+1)個で、正方形を作る碁石は(n+1)2個だから、碁石は全部で{(n+1)2-7}個だね。
方程式を作るとn2+20=(n+1)2-7で、右辺を展開するとn2+20=n2+2n+1-7だから、n2が消えて2n=26よりn=13がわかる。したがって、碁石は全部で132+20=189(個)だよ。
中空方陣で碁石の数を求めるには?
(2)は中空方陣の問題です。中空方陣で碁石の数を求める場合、重なる部分ができないように碁石を四等分しましょう。
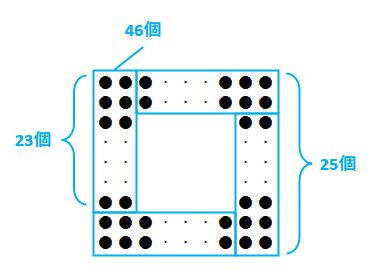
図3の正方形は、下の図のように碁石を四等分します。189÷4=47あまり1ですが、碁石が2周しているので、四等分したうちの1つ分の碁石の数は偶数の46です。したがって、正方形の一辺に並ぶ碁石は46÷2+2=25(個)です。
また、あまった碁石は189-46×4=5(個)です。

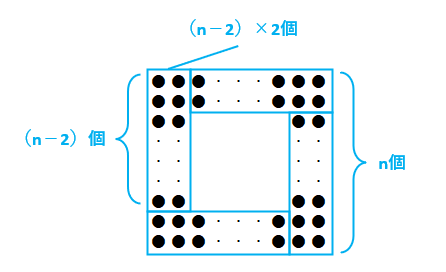
図3の正方形の一辺に並ぶ碁石をn個とすると、正方形を作る碁石は(n-2)×2×4だよ。(n-2)×2×4=189として、8n=205よりn=205÷8=25あまり5になる。したがって、正方形の一辺に並ぶ碁石は25個で、あまった碁石は5個だよ。
規則性の問題で碁石の数を求めるには?
狸雄は、知玄に突き付けられた【問題1】を解き、ホッとしていました。
そこに現れたのは色白の老人「知白(ちはく)」です。知白も狸雄に【問題2】を突き付けて、「解けねば、呪われるぞ!」と脅してきます。

迷惑なじいさんがもう一人現れたよ。最悪!
【問題2】下の図のように、あるきまりにしたがって、白い碁石と黒い碁石を並べて正方形を作っていきます。それぞれの正方形を1番目、2番目、…とします。
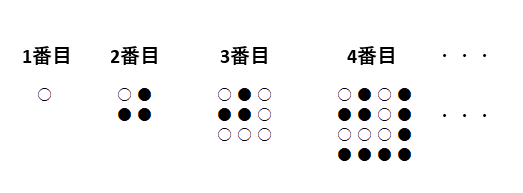
(1) 15番目の正方形に並べた白い碁石は何個ですか。
(2) 白い碁石と黒い碁石の数の和が初めて1000個を超えるのは何番目の正方形ですか。また、この正方形に並べた黒い碁石は何個ですか。
【問題2】のように、碁石をあるきまりにしたがって並べる問題は、数列の知識を利用して解くのが簡単です。そのため、具体的に碁石の数を数え上げ、どのような数列になっているかをとらえることからスタートしましょう。
白い碁石の数を求めよう
(1)では白い碁石の数を求めます。そのため、白い碁石の数が増える奇数番目に注目して、具体的に白い碁石の数を数え上げます。5番目の正方形は図にありませんが、4番目の正方形に白い碁石を書き加えてみましょう。
- 1番目:1個
- 3番目:1+5=6(個)
- 5番目:1+5+9=15(個)
1、5、9、…は、はじめの数(初項)が1、増える数(公差)が4の等差数列です。つまり、奇数番目の正方形に並べた白い碁石の数は等差数列の和になっています。
15は、1から数えて8個目の奇数です。したがって、(1)では、等差数列の和が8個の数の和となって、1+5+9+13+17+21+25+29=(1+29)×8÷2=120(個)です。(等差数列の和の公式「(はじめの数+おわりの数)×個数÷2」を使いました)
碁石の数の和を求めよう
(2)では、並べた白い碁石と黒い碁石の数の和をまずは考えます。白い碁石と黒い碁石の数の和は平方数なので、1000に近い平方数を考えます。
30×30=900より、31番目か32番目で和が1000個を超えると見当を付けましょう。31×31=961、32×32=1024なので、和が1000個を超えるのは32番目の正方形です。
(1)と同じように、黒い碁石の数が増える偶数番目に注目して、具体的に黒い碁石の数を数え上げます。
- 2番目:3個
- 4番目:3+7=10(個)
- 6番目:3+7+11=21(個)
偶数番目の正方形に並べた黒い碁石の数は、はじめの数が3、増える数が4の等差数列の和になっています。
32は、2から数えて16個目の偶数です。したがって、32番目の正方形に並べた黒い碁石の数は、3個から、3+4×(16-1)=63(個)までの和です。(等差数列のn番目の数を求める公式「はじめの数+加える数×(n-1)」を使いました)
以上より、32番目の正方形に並べた黒い碁石は(3+63)×16÷2=528(個)です。(等差数列の和の公式「(はじめの数+おわりの数)×個数÷2」を使いました)

おいらが問題に正解したから知玄と知白はようやく退散したけど、この2人はいったい何者なんだろう?
知玄と知白はいったい何者なのか?
謎の老人コンビ・知玄と知白は囲碁の精です。江戸時代の小説家・林義端(はやしぎだん)の怪異小説『玉箒木(たまははき)』などに登場します。
江戸・牛込に住む清水昨庵は囲碁が大好きでした。あるとき、近所の円照寺を散歩していた昨庵は、色黒で山辺に住む知玄と、色白で海辺に住む知白に出会いました。この後、昨庵は囲碁の名人となったそうです。
囲碁の精といえば、『週刊少年ジャンプ』で連載されていた人気漫画『ヒカルの碁』を思い出す読者もいるはずです。主人公の少年・進藤ヒカルは、天才棋士の亡霊・藤原佐為(ふじわらのさい)に取り憑かれたことがきっかけで囲碁を始め、「神の一手」を目指して成長していきます。藤原佐為は女性と見まがうほどの美しい容姿で、老人の姿ではありません。そのビジュアルの虜になった女性ファンも多いでしょう。






コメント