高校2年生の幽美狐はクラスメイトの舞理から声をかけられました。

おまえは2週間後、この世にいない。

あなた、しつこいわね。いつもいつも私に呪いをかけて楽しい?

おまえがいるから霧斗先輩はあたしのことを見てくれない。おまえさえいなければ……。呪ってやるっ!

はいはい、お好きにどーぞ。
幽美狐に軽くあしらわれた舞理ですが、今度こそ呪いを成就させるため、オリジナルの呪い人形を作りました。
そんな舞理と一緒に、数列の基礎である等差数列について学びましょう。n番目の数や和を求める公式が成り立つ理由を説明できますか?
等差数列はどんな数列なの?
【問題】舞理は幽美狐に呪いをかけるため、オリジナルの呪い人形を作り、あるきまりにしたがって人形に待ち針を刺していきます。呪い人形に刺さった待ち針の本数は次の通りです。
| 日数 | 1日目 | 2日目 | 3日目 | 4日目 | ・・・ |
|---|---|---|---|---|---|
| 待ち針の本数 | 5本 | 8本 | 11本 | 14本 | ・・・ |
(1) 2週間後(14日目)、呪い人形に刺さった待ち針は何本ですか。
舞理はより強い呪いをかけるため、毎日新しく呪い人形を作り、1体目の人形と同じきまりで待ち針を刺していくことにしました。
たとえば、2日目の人形の数は、待ち針が8本刺さった人形、5本刺さった人形の2体です。3日目の人形の数は、待ち針が11本刺さった人形、8本刺さった人形、5本刺さった人形の3体です。
(2) 2週間後(14日目)、すべての呪い人形に刺さった待ち針は合計で何本ですか。
【問題】に「あるきまりにしたがって」と書かれているので、そのきまりを明らかにしましょう。中学受験算数ではまず、差を求めてみるのがおすすめです。
待ち針の本数について、2日目と1日目の差は3本、3日目と2日目の差は3本、4日目と3日目の差は3本です。つまり、待ち針の本数が3本ずつ増えています。
このように、一定の数を次々と加えていく(引いていく)数列が「等差数列」です。【問題】の待ち針の本数は、はじめの数が5、加える数が3の等差数列になっています。
n番目の数の公式が成り立つのはなぜ?
(1)は、たった14個なので、地道に3を足していっても答えを求められます。しかし、今後の数列の勉強につながるように、規則性に注目して計算で答えを求めましょう。
「はじめの数の5に3をいくつ足しているか?」がわかるように待ち針の本数を書き出すと次の通りです。
- 1日目 … 5
- 2日目 … 5+3×1
- 3日目 … 5+3×2
- 4日目 … 5+3×3
書き出した結果、5+3×(日数-1)となっていることがわかりました。したがって、2週間後(14日目)の待ち針の本数は5+3×(14-1)=44(本)です。

4は「死」と結び付く数字よ。そんな縁起の悪い数字が2つ続くなんて……。幽美狐の命が尽きるのも時間の問題ね、フフフ……。
5、8、11、14、…のような等差数列について、左の数から1番目、2番目、3番目、4番目、…とします。このとき、(1)の解説から、n番目の数を次の公式で表せることがわかるでしょう。
たとえば、3、5、7、9、…は、はじめの数が3、加える数が2の等差数列です。この等差数列に公式①を使うと、32番目の数は3+2×(32-1)=65、555番目の数は3+2×(55-1)=1111、2024番目の数は3+2×(2024-1)=4049です。

高校数学では、等差数列のはじめの数を「初項」、加える数を「公差」、n番目の数を「一般項」というのよ。だから、初項a、公差dの等差数列の一般項はan=a+(nー1)dと表されるわ。
和の公式が成り立つのはなぜ?
(2)の2週間後(14日目)の人形の数は、待ち針が44本刺さった人形、41本刺さった人形、38本刺さった人形、…、5本刺さった人形の14体です。すべての呪い人形に刺さった待ち針は合計で44+41+38+…+5(本)です。
式の数字を逆にした5+8+11+…+44は、はじめの数が5、加える数が3の等差数列の1番目から14番目までの数の和になっています。
さて、5+8+11+…+44と、順序が逆の44+41+38+…+5を以下のように足してみましょう。
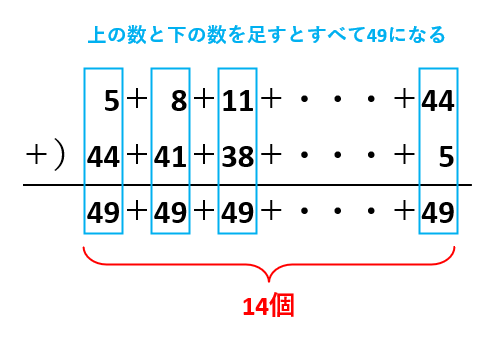
49×14=(5+8+11+…+44)×2なので、5+8+11+…+44=49×14÷2=343(本)が(2)の答えです。

「死」と結び付く4と、「苦」と結び付く9を組み合わせた49が14個、つまり「十分に死ぬ」ってわけ! これで幽美狐は終わりね。フフフ……。
順序を逆にした和を足していくことで、等差数列の和を次の公式で表せます。
たとえば、3+5+7+9+…に公式②を使うと、1番目から32番目までの数の和は(3+65)×32÷2=1088、555番目までの数の和は(3+1111)×555÷2=309135、2024番目までの数の和は(3+4049)×2024÷2=4100624です。

高校数学では、おわりの数を「末項」、個数を「項数」というわ。等差数列の初項aから末項ℓまでの項数がnのとき、その和はSn=\(\frac{1}{2}\)n(a+ℓ)よ。
さらに、公差dがわかってるなら、末項ℓ=a+(n-1)dなので、これをSnの式に代入して、Sn=\(\frac{1}{2}\)n{2a+(n-1)d}とも表せるのよ。

舞理、何一人でブツブツ言ってるのよ?

おまえはどうして生きてる? あたしの呪いは2週間後に成就するなのに……。

あなたの呪いなんて効くわけないじゃん。それより、その手の包帯はどうしたの?

呪い人形に待ち針を刺してるとき、まちがって自分の指に刺しちゃったのよ。

「人を呪わば穴二つ」ってことね。これに懲りて、薄気味悪いことするの、やめたら?

黙れっ! 次こそは必ずおまえの息の根を止めてやるっ!






コメント