高校2年生の幽美狐は、神秘的な力が宿っているパワーストーンが大好きです。そんな幽美狐がパワーストーンショップを訪れました。
パワーストーンの個数と金額から、中学受験算数の「消去算」を学びましょう。

パワーストーンショップのイメージ
消去算とはどのような特殊算か?
【問題】幽美狐はパワーストーンショップでパワーストーンを買うつもりです。(1)から(3)のことがわかっているとき、パワーストーン1個の値段はそれぞれいくらですか。
(1) クリスタル3個とサーペンティン2個で840円、クリスタル5個とサーペンティン2個で1160円です。
(2) カーネリアン3個とアメジスト2個で860円、カーネリアン2個とアメジスト5個で1050円です。
(3) オニキス2個とアマゾナイト3個で980円、オニキス1個はアマゾナイト1個よりも40円高いです。
【問題】のようにわからない数がいくつかあるとき、式を作ってこれらの数を求めるのが消去算です。
消去算の解き方には加減法と代入法があります。どちらの解き方も「消去=消し去ること」がポイントです。消去算では「どれを消去できるかな?」と常に考えましょう。

消去算は中学数学の連立方程式と全く同じよ。連立方程式を理解できない中学生は、消去算で具体的なイメージをつかむといいと思うわ。
消去算を加減法で解く
加減法は、式同士を足したり引いたりして消去する方法です。
個数がそろっているものがある場合
(1)の式を下の図で表しました。
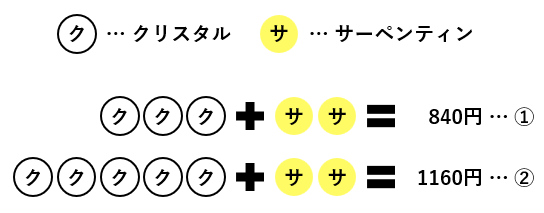
①の式と②の式を見比べると、サーペンティンの個数が2個でそろっていることがわかります。個数がそろっているものがある場合、これを消去するために式同士の引き算をします。下の図のように②から①を引きましょう。
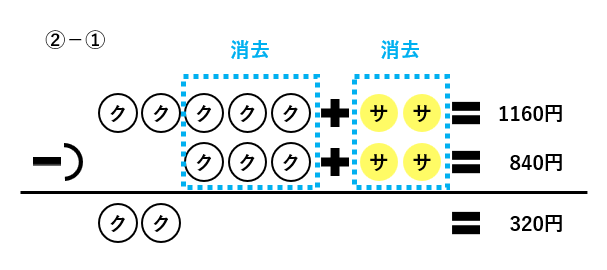
②-①の結果、クリスタル2個の値段が320円だとわかりました。したがって、クリスタル1個の値段は320÷2=160(円)です。
続いて、クリスタル1個が160円なので、クリスタル3個で160×3=480(円)です。下の図のように、クリスタル3個を480円でおきかえます。このおきかえが代入です。
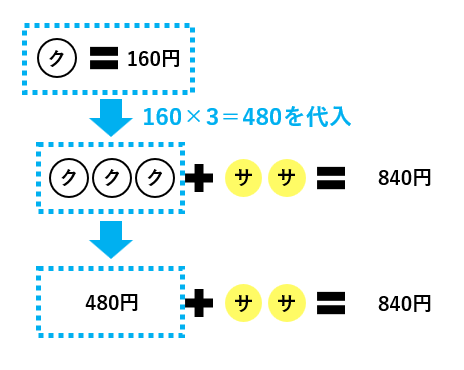
クリスタル3個に480円を代入した結果、サーペンティン2個の値段が840-480=360(円)だとわかりました。したがって、サーペンティン1個の値段は360÷2=180(円)です。
以上より、クリスタル1個の値段は160円、サーペンティン1個の値段は180円です。
消去算を解くとき、ここまでの説明みたいに図をいちいち描くのは大変です。そこで、次のように、式を書いて計算で解くのが普通です。
クリスタル1個の値段を「ク」円、サーペンティン1個の値段を「サ」円とすると
- ク×3+サ×2=840 … ①
- ク×5+サ×2=1160 … ②
②-①より
- ク×2=320
- ク×1=320÷2=160
ク×1=160を①に代入して
- 160×3+サ×2=840
- サ×2=840-480=360
- サ×1=360÷2=180
したがって、クリスタル1個の値段は160円、サーペンティン1個の値段は180円
どちらかの個数を最小公倍数にそろえる場合
(2)も、(1)と同じように式を作ってみましょう。
カーネリアン1個の値段を「カ」円、アメジスト1個の値段を「ア」円とすると
- カ×3+ア×2=860 … ①
- カ×2+ア×5=1050 … ②
①と②を見比べると、カーネリアンもアメジストも個数がそろっていません。個数がそろっているものがない場合、どちらかの個数を最小公倍数にそろえます。
今回は、カーネリアンの個数を3と2の最小公倍数6にそろえましょう。①全体を2倍、②全体を3倍します。
- ①×2より、カ×6+ア×4=1720 … ③
- ②×3より、カ×6+ア×15=3150 … ④

=の右側(右辺)を2倍や3倍にするのを忘れやすいので要注意です。カ×6+ア×4=860とすると、=の左側(左辺)の個数が増えたのに、合計の値段が①と同じになります。これだと、等式が成り立たなくなることを理解しましょう。
④-③より
- ア×11=1430
- ア×1=1430÷11=130
ア×1=130を①に代入して
- カ×3+130×2=860
- カ×3=860-260
- カ×1=600÷3=200
したがって、カーネリアン1個の値段は130円、アメジスト1個の値段は200円

アメジストの個数を2と5の最小公倍数10にそろえて計算しても同じ結果になるわ。ぜひ試してみてね。
代入法で消去算を解く
代入法は、一方の式をもう一方の式に代入して消去する方法です。既に何度か出てきましたが、代入はおきかえることです。
(3)も、まずは式を作ってみましょう。
オニキス1個の値段を「オ」円、アマゾナイト1個の値段を「ア」円とすると
- オ×2+ア×3=980 … ①
- オ×1=ア×1+40 … ②

40を足すのか引くのか、わからなくなるんですけど……。

そういうときは、具体的な数字で考えてみましょう。たとえば、「60円は20円よりも40円高いです」という場合、60と20と40の関係を表した等式は、60=20+40と60=20-40のどっちが正しいですか?

60=20+40ですね。あっ、この60をオ×1に、20をア×1にすればいいんですね!
②の式では、=の両側にオ×1とア×1があります。このように、=の両側(両辺)にわからない数がある式を見たら代入法を使うといいでしょう。
注意すべきポイントは、下の図のように、②を①に代入するとき、ア×1+40に( )をつけて2倍することです。( )を外すときに分配法則を使って、(ア×1+40)×2=ア×2+80となります。40×2を忘れないようにしましょう。
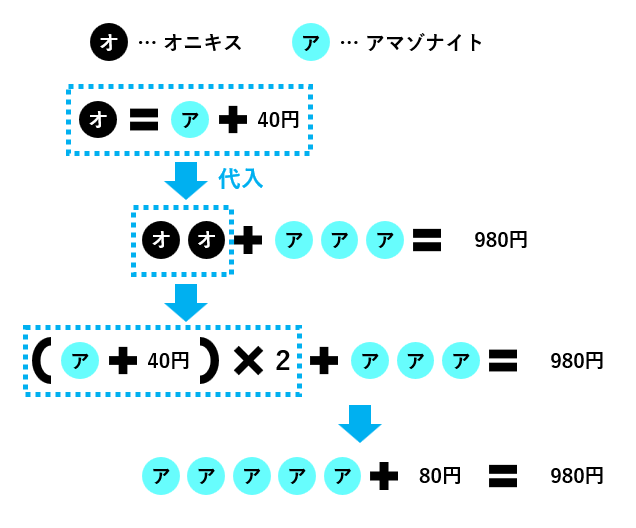
この図を式で表して最後まで計算すると次の通りです。
②を①に代入して
- (ア×1+40)×2+ア×3=980
- ア×2+80+ア×3=980
- ア×5=980-80
- ア×1=900÷5=180
ア×1=180を②に代入して
- オ×1=180×1+40=220
したがって、オニキス1個の値段は220円、アマゾナイト1個の値段は180円

消去算はさまざまな文章題を計算で解くのに使える便利なツールです。実はつるかめ算も消去算で解けます。実際の入試では、線分図や面積図を描くのが大変な問題も出題されます。そういう問題でこそ消去算が役立ちます。





コメント