霊感がある人は、幽霊のような、本来は目に見えない存在を感じ取ることがあります。視覚・聴覚・触覚・味覚・嗅覚の五感に加えて、これらとは異なる「第六感」が発達していると考えられます。
そんな霊感に興味を持った狸雄は、自分が通う中学校の3年生について、霊感がある生徒が何人いるかを調べました。この調査を通して、多くの中学受験生が苦手とする割合の基礎を学びましょう。
割合とはいったい何なのか?
【問題】狸雄が通う中学校の3年生全体の人数は192人です。そのうち24人の生徒が「霊感がある」と自覚していました。
(1) 「霊感がある」と自覚している生徒は3年生全体の何%ですか。
(2) 「霊感がある」と自覚している生徒のうち、男子の人数は女子の人数の\(\frac{3}{5}\)です。このとき、「霊感がある」と自覚している女子は何人ですか。
【問題】は割合に関する問題です。多くの中学受験生は「割合は難しい」と思い込んでいますが、割合の意味さえわかれば決して難しくありません。
割合は「セット」の考え方と同じ
「割合とはいったい何なのか?」を考える前に、下の図を見てください。
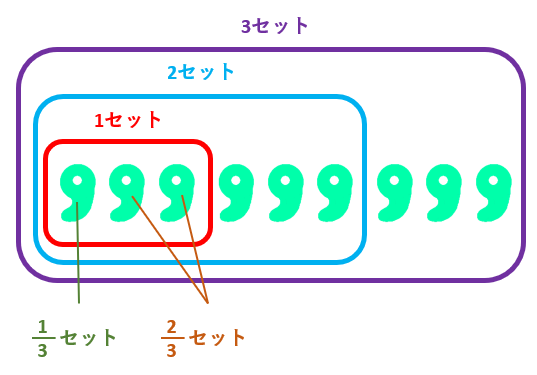
9個の勾玉のうち、3個を1セットにします。そうすると、6個は2セット、9個は3セットになります。一方、2個は「3個に分けたうちの2個」なので\(\frac{2}{3}\)セット、1個は「3個に分けたうちの1個」なので\(\frac{1}{3}\)セットと表せるでしょう。
この「セット」の考え方と割合は同じです。割合は「ある数を1にしたとき、他の数がいくつになるか?」を表しています。上の図では、3個を1にしたとき、6個の割合は2です。この2に「倍」をつけて「6個は3個の2倍です」ということもあります。「倍」の考え方が割合の基本です。
割合では、1にする数を「もとにする量」、他の数を「比べられる量」といいます。割合の問題では、もとにする量を見つけましょう。もとにする量と割合以外の数が比べられる量です。
上の図で「3個をもとにしたとき、2個の割合は\(\frac{2}{3}\)です」と書かれていれば、もとにする量が3であるとすぐにわかります。一方、「2個は3個の\(\frac{2}{3}\)です」「3個の\(\frac{2}{3}\)は2個です」などと書かれている場合、割合(\(\frac{2}{3}\))の前にある「の」の前の数(3)がもとにする量です。
割合・もとにする量・比べられる量の関係
上の図で、勾玉3個が1セットなので、2セットにすれば勾玉が3×2=6(個)になります。同じように、もとにする量に割合をかければ比べられる量を求められます。逆に、比べられる量を割合で割ればもとにする量になり、比べられる量をもとにする量で割れば割合になります。
これらの関係を下の式にまとめて「割合の3用法」とすることがあります。必要ならば「もとにする量×割合=比べられる量」だけ覚えて、他の2つは式変形で導けば十分です。
- もとにする量×割合=比べられる量
- 比べられる量÷割合=もとにする量
- 比べられる量÷もとにする量=割合
もっとも、これらの式を丸暗記するよりも、線分図などを描いてその場で関係をとらえた方がわかりやすいでしょう。
割合・百分率・歩合の関係
もとにする量を1にすると、割合が分数や小数になってイメージしにくくなります。そこで、もとにする量を1以外の数にしたのが百分率と歩合(ぶあい)です。
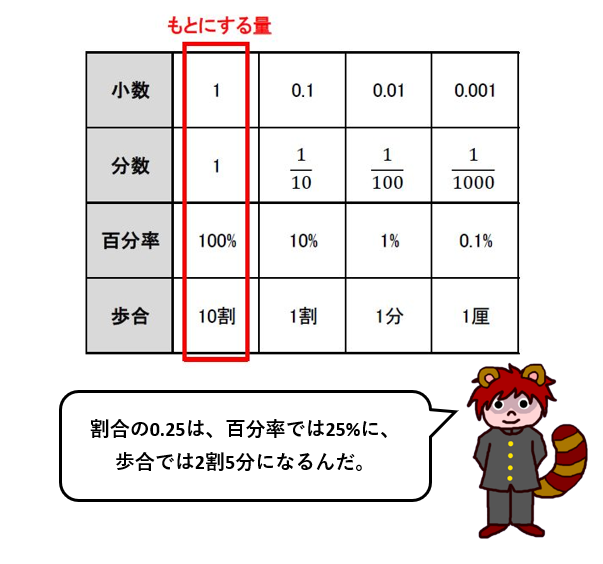
百分率では、もとにする量を100%にします。一方、歩合では、もとにする量を10割にします。歩合は、1割の\(\frac{1}{10}\)を1分(ぶ)、1分の\(\frac{1}{10}\)を1厘(りん)で表します。
割合(分数・小数)・百分率・歩合の関係は下の表で確認してください。
割合の問題を線分図で解く
割合の問題は、割合の3用法や「くもわ」などの図を使わなくても、線分図を描くと簡単に解けます。
(1)は、「何%」が割合なので、その前にある「の」の前の「3年生全体(192人)」がもとにする量です。さらに、割合に%がついていて百分率とわかるので、192人=![]() として、下の図のような線分図を描きます。上の段には人数を、下の段には百分率をそれぞれ書き込みました。
として、下の図のような線分図を描きます。上の段には人数を、下の段には百分率をそれぞれ書き込みました。
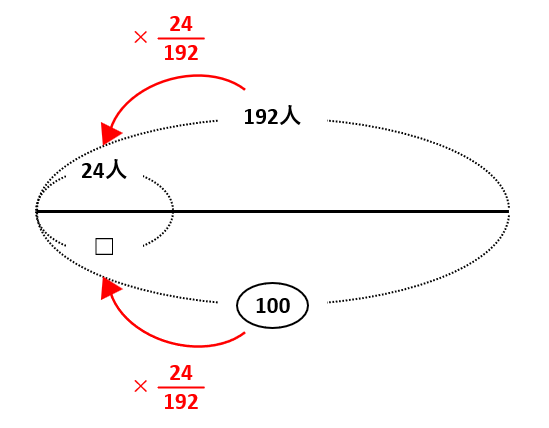
上の段と下の段は比例関係にあります。上の段で192×\(\frac{24}{192}\)=24なので、下の段で□=100×\(\frac{24}{192}\)=12.5(%)が答えです。
「比べられる量÷もとにする量=割合」の式に、比べられる量=24、もとにする量=194を当てはめて割合=0.125を求めた後、0.125×100=12.5(%)でも答えになります。

線分図に割合・百分率・歩合を書き込むときは、○や□、△などで囲って、普通の数字とは区別しましょう。
(2)は、「\(\frac{3}{5}\)」が割合なので、その前にある「の」の前の「(『霊感がある』と自覚している)女子の人数」がもとにする量です。「『霊感がある』と自覚している生徒の人数」がもとにする量ではないので注意しましょう。
「(『霊感がある』と自覚している)女子の人数」を①として、下の図のような線分図を描きます。
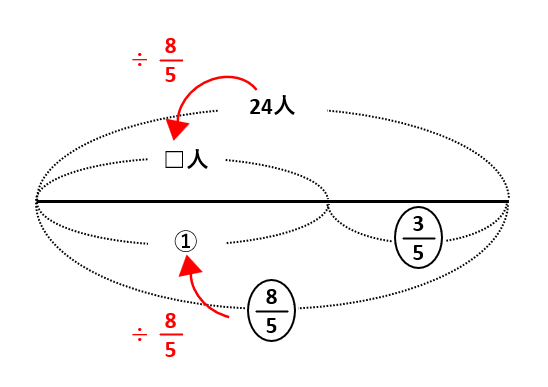
下の段で\(\frac{8}{5}\)÷\(\frac{8}{5}\)=1なので、上の段で□=24÷\(\frac{8}{5}\)=15(人)が答えです。
「比べられる量÷割合=もとにする量」の式に、比べられる量=24、割合=\(\frac{8}{5}\)を当てはめて割合=24÷\(\frac{8}{5}\)=15(人)でも答えになります。
分数の割合を整数に直して解く
(2)は、分数の割合を整数に直して解くこともできます。
\(\frac{3}{5}\)は「5個に分けたうちの3個分」という意味なので、これを③にすると、もとにする量の1は⑤になります。そうすると、下の線分図のように⑧=24人とわかり、①=3人となって□=⑤=3×5=15(人)という答えを求められます。
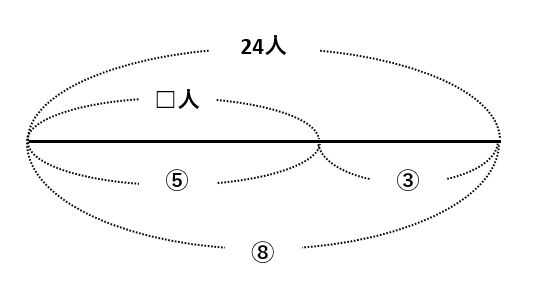
分数の割合を整数に直して解くと、イメージがつかみやすくなって、計算も楽です。さらに、後で学ぶ比の練習にもなります。

うわっ、幽霊が出たっ!

人間に化けたタヌキに驚かれるなんて心外だわ。





コメント