神秘的な力が宿っている石が「パワーストーン」です。パワーストーンは、持ち主の願いをかなえたり、持ち主を災いから守る魔除けになったりするといわれます。
そんなパワーストーンが大好きな高校2年生の幽美狐と一緒に、中学受験算数の「場合の数」の基本を学びましょう。数学の「場合の数」が苦手な中学生や高校生にも役立つ内容です。
場合の数には順列と組合せがある
【問題】幽美狐はターコイズ、アメジスト、ラピスラズリ、サファイア、ガーネットの5種類のパワーストーンを1個ずつ持っています。
(1) 幽美狐は寝る前、5種類のパワーストーンの中から2個を選び、それぞれ机の上とベッドの枕元に置きます。パワーストーンの置き方は何通りですか。
(2) 幽美狐は出かけるとき、5種類のパワーストーンの中から2個を選び、これらをカバンの中に入れて持ち歩いています。パワーストーンの選び方は何通りですか。
(3) 幽美狐は模擬試験の日、5種類のパワーストーンの中から3個を選び、これらをカバンの中に入れることにしています。パワーストーンの選び方は何通りですか。
人やものの並べ方や選び方を考えるのが「場合の数」です。場合の数には大きく分けて次の2種類があります。
- 順列 … 並び順を考える。
- 組合せ … 並び順を考えない。
たとえば、6年3組の30人の中から5人を選んで一列に並ばせるなら順列です。A君、B君、C君、D君、E君の5人を並ばせるとすると、ABCDEとEDCBAはどちらも並び方が違うからです。一方、30人の中から5人を選んでチームを作るなら組合せです。ABCDEとEDCBAは同じ選び方だからです。
このように、場合の数の問題では、順列と組合せのどちらなのかを正しく判断することがとても大切です。
【問題】の(1)では、ターコイズとアメジストを選んだとき、次の2つの置き方は違います。
- 机の上にターコイズを置いて、ベッドの枕元にアメジストを置く。
- 机の上にアメジストを置いて、ベッドの枕元にターコイズを置く。
このことから、ターコイズとアメジストの並び順を考えることと同じといえます。したがって、(1)は順列です。
一方、(2)と(3)では、選んだ石はすべて同じカバンの中に入れるので、石の並び順を考える必要はありません。したがって、(2)と(3)は組み合わせです。
場合の数の問題を樹形図で解く
場合の数の問題を解くときに役立つのが樹形図です。樹形図は、樹木のように枝分かれしていく図で、すべての場合を書き出すときに使います。
【問題】の(1)の樹形図は以下の通りです。ターコイズ、アメジスト、ラピスラズリ、サファイア、ガーネットをそれぞれタ、ア、ラ、サ、ガと表しました。
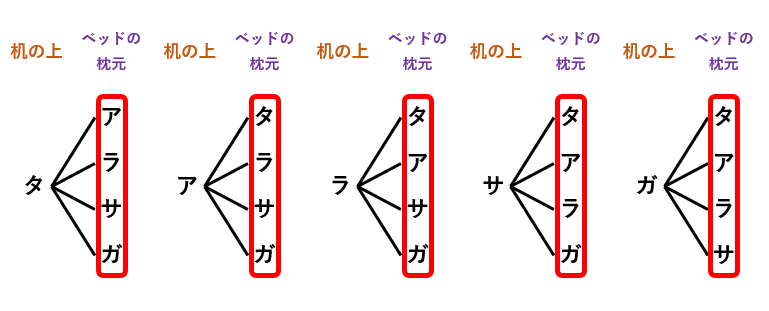
赤枠で囲った部分を数えて20通りが答えです。
樹形図を描くときは、規則正しく書いていくことで重複や抜け漏れを防げます。(1)では、タアラサガの順番をできるだけ崩さないように、規則正しく書いていきました。
(2)は(1)と違う樹形図になります。
たとえば、ターアとアータは同じ選び方なので、ターアを書いたらアータを書いてはいけません。タアラサガの順番で考えるなら、アの枝の先には、アの右側にあるラサガだけを書きます。同じように、ラの枝の先には、ラの右側にあるサガだけを書きます。
このことをふまえて(2)の樹形図を描くと以下の通りです。
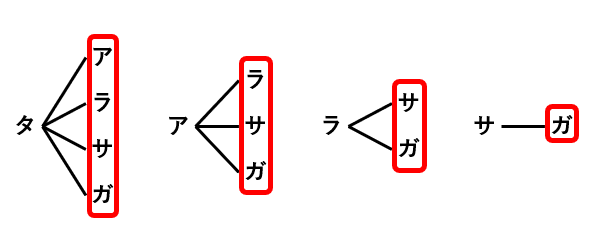
赤枠で囲った部分を数えて10通りが答えです。
(3)でも樹形図を描くのはちょっと面倒です。ここで発想の転換をします。「5個の中から、カバンに入れる3個を選ぶ」ことは、「5個の中から、カバンに入れない2個を選ぶ」ことと同じです。なぜなら、「カバンに入れない2個」を選べば、残り3個をカバンに入れることになるからです。
つまり、(2)と(3)は同じことをすればいいだけだとわかります。したがって、樹形図を描くまでもなく、(3)の答えは(2)と同じ10通りです。
場合の数の問題を計算で解く
場合の数の問題を解くとき、いちいち樹形図を描くのは面倒です。計算で解ける問題は計算で解いてしまった方が楽でしょう。
【問題】の(1)では、まず、机の上に置く石の選び方は5通りです。次に、ベッドの枕元に置く石の選び方は、机の上に置いた石を除いた4通りです。
たとえば、机の上にターコイズを置いたとすると、ベッドの枕元にはアメジスト、ラピスラズリ、サファイア、ガーネットの4個の中からどれか1個を置けます。同じように考えれば、机の上に置く石の5通りの選び方それぞれについて、ベッドの枕元に置く石の選び方が4通りずつあることがわかるでしょう。
したがって、5通りと4通りをかけて5×4=20(通り)が答えです。

高校数学の「場合の数」では、「異なるn個のものをすべて1列に並べる場合の数はn!=n×(n-1)×(n-2)×…×3×2×1」と表して、これを「nの階乗」と呼ぶわ。そして、「異なるn個のものの中からr個を取り出して1列に並べる順列の数」は次の公式になるの。
$${}_{ n }P_{ r }=\frac{n!}{(n-r)!}$$$$=\underbrace{ n \times (n-1) \times (n-2) \times \cdots }_{r個}$$
Pはパーミュテーション( permutation )の頭文字よ。Pなんて出てくると混乱しちゃうけど、公式の意味は中学受験算数でやってることと全く同じね!
(1)では、どの2つの石を選んでも、それぞれで2通りの並び順を数えています。一方、(2)では、これらの2通りの並び順を同じと考えます。
たとえば、(1)では「ターコイズ→アメジスト」と「アメジスト→ターコイズ」の2通りの並び順を区別しますが、(2)ではこの2通りを区別せずに1通りとします。
したがって、(1)の答えを2で割って、20÷2=10(通り)が(2)の答えです。
(3)も、まず、5種類の石の中から3個を選んで一列に並べて、5×4×3=60(通り)を求めます。次に、選んだ3種類の石の並び順を考えて、3×2×1=6(通り)を求めます。これら6通りは区別せずに1通りとするので、60÷6=10(通り)が答えです。
(2)と(3)からわかる通り、組合せの問題は、順列として計算した結果を、選んだものの個数の並び順で割ります。2個のものを選んだら2×1=2で、3個のものを選んだら3×2×1=6で、4個のものを選んだら4×3×2×1=24で、それぞれ割ります。

高校数学では「異なるn個のものの中からr個を取り出す組合せの数」を次の公式で表すわ。
$${}_{ n }C_{ r }=\frac{{}_{ n }P_{ r }}{r!}=\frac{n!}{r!(n-r)1}$$
Cはコンビネーション( combination )の頭文字よ。分母のr!は「r個のものの並び順で割る」って意味ね。
パワーストーンにはどんな効果がある?
算数とは関係ありませんが、幽美狐が持っているパワーストーンの効果を紹介します。
| 名前 | 特徴・伝承 | 効果 |
|---|---|---|
| ターコイズ | 12月の誕生石。青や緑に黒い線模様が不規則に走る。エジプトやメソポタミアなどの古代文明でも宝石として大切にされてきた。14世紀頃には、トルコ商人が貿易で広めたことから「トルコ石」とも呼ばれる。 | 旅の安全・繁栄・厄除け |
| アメジスト | 2月の誕生石。半透明の紫色で、「紫水晶」とも呼ばれる。石英に微量の鉄イオンを含んでいる。名前の由来となったギリシャ語の「アメテュストス」は、「酒に酔わない」という意味がある。 | 真実の愛・心の調和・厄除け |
| ラピスラズリ | 12月の誕生石。青色に黄色い斑点模様が混ざる。古代より装飾品や顔料などに使われてきた。国や時代を超えて、さまざまな価値を付与されて珍重されている。 | 成長・幸福・厄除け |
| サファイア | 9月の誕生石。深い青色で、ダイヤモンドの次に硬い。フランスの初代皇帝ナポレオンは、浮気者の妻ジョゼフィーヌにサファイアを贈った。当時「皇帝の石」と呼ばれていたサファイアを手放したナポレオンは、後に衰退の一途をたどることとなる。 | 知性・カリスマ性・浮気封じ |
| ガーネット | 1月の誕生石。深い赤色で、結晶がザクロの実に似ているため「柘榴石」とも呼ばれる。『旧約聖書』の「ノアの箱舟」の物語では、ガーネットが輝いて暗闇を照らし、箱舟の行き先を示したという。 | 勝利・情熱・一途な愛 |

webムーによると、古代エジプト文明では、天空と冥界の神オシリスの象徴であるラピスラズリをツタンカーメン王の黄金マスクに使用し、魂の再生を願っていたそうよ。






コメント