神秘的な力が宿っている石であるパワーストーンは、ブレスレットやネックレスなどの材料としても使われます。
そんなパワーストーンを題材として、中学受験算数の「場合の数」によく出る円順列と数珠(じゅず)順列を解説します。
円順列や数珠順列とは何か?
【問題】幽美狐はターコイズ、アメジスト、ラピスラズリ、サファイア、ガーネットの5種類のパワーストーンを1個ずつ持っています。
(1) 幽美狐は5種類のパワーストーンを机の上に円の形に並べます。パワーストーンの並べ方は何通りですか。
(2) 幽美狐は5種類のパワーストーンをひもでつないでブレスレットを作ります。パワーストーンのつなぎ方は何通りですか。
(3) 幽美狐はターコイズ2個、アメジスト2個、ラピスラズリ1個をひもでつないでブレスレットを作ります。パワーストーンのつなぎ方は何通りですか。
(1)は、回転させると一致する並べ方を同じものと考える円順列の問題です。たとえば、下の2つの並べ方は同じものになります。ターコイズ、アメジスト、ラピスラズリ、サファイア、ガーネットをそれぞれタ、ア、ラ、サ、ガと表しました。
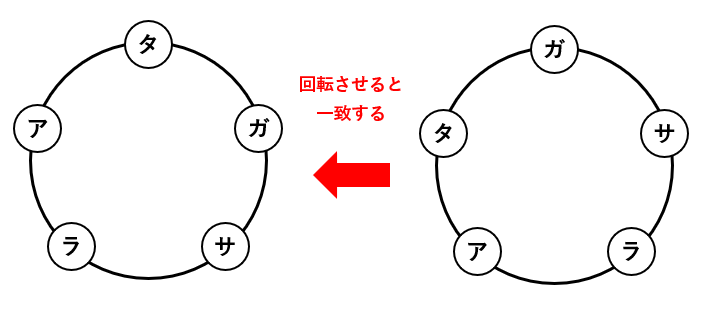

パワーストーンを円の形に並べるとき、ターコイズを西側に置くのか東側に置くのかは違う並べ方だと思います。

幽美狐さんの言うことはその通りです。実際、何人かが円の形に座る場合、どの席に座るかが重要であることも多いでしょう。でも、算数や数学の世界では、特別な断りがない限り、回転させると一致する並べ方は同じものと考えます。
一方、(2)や(3)は、回転させることに加えて、裏返すと一致する並べ方も同じものと考える数珠(じゅず)順列の問題です。たとえば、下の2つの並べ方は同じものになります。
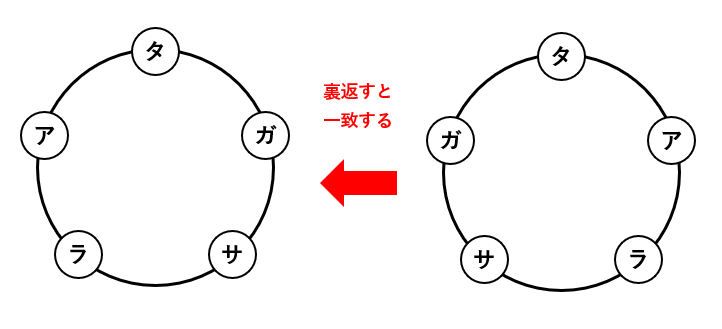
ちなみに、数珠は、珠に穴をあけて糸を通した仏具で、お坊さんがお経を唱えるときなどに手にかけて使います。
円順列の問題を解く
円順列の問題では、回転しないようにするため、どれか1つを固定するのがポイントです。
(1)では、下の図のようにターコイズ(タ)を固定して、他の位置を①~④とします。
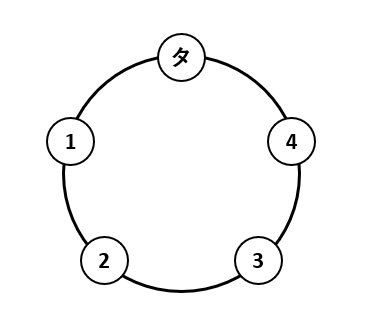
- ①に置ける石は、ターコイズを除いた4通りです。
- ②に置ける石は、ターコイズと①に置いた石を除いた3通りです。
- ③に置ける石は、ターコイズと①②に置いた石を除いた2通りです。
- ④に置ける石は、ターコイズと①②③に置いた石を除いた1通りです。
したがって、4×3×2×1=24(通り)が答えです。

高校数学の「場合の数」では、「異なるn個のものをすべて1列に並べる場合の数はn!=n×(n-1)×(n-2)×…×3×2×1」と表すけど、「異なるn個のものをすべて円形に並べる円順列の数は(n-1)!」よ。
(1)も公式に当てはめると、(5-1)!=4!=4×3×2×1=24(通り)だわ。
数珠順列の問題を解く
異なるものをつなぐ数珠順列では、裏返すと同じつなぎ方が2通りずつ出てきます。このような数珠順列では、円順列を考えた後に2で割ると答えを求められます。
(2)は、(1)の答えを2で割って、24÷2=12(通り)が答えです。
同じものを含む数珠順列の問題を解く
(3)は(2)と違って、すべての石が異なるわけではなく、同じ石がいくつか含まれています。このような数珠順列の問題は、(2)のように単純に2で割っても正しい答えを求められません。
(3)は石が5個しかないので、下の図のように、すべてのつなぎ方を描いて数えるのが楽でしょう。このときのポイントは、1個しかないラピスラズリを一番上に固定してしまうことです。4通りが答えだとわかります。

(3)を計算で求めることもできますが、却って面倒です。
計算で求める場合も、1個しかないラピスラズリを一番上に固定してしまいます。その後、残った石のつなぎ方を考えます。
ターコイズとアメジストのつなぎ方は、まず、すべての石が異なると考えて4×3×2×1=24(通り)です。次に、ターコイズ2個は区別しないので、その並び順である2通りで24通りを割って24÷2=12(通り)にします。アメジストも同じように考えて12÷2=6(通り)です。この6通りをすべて描くと下の図になります。
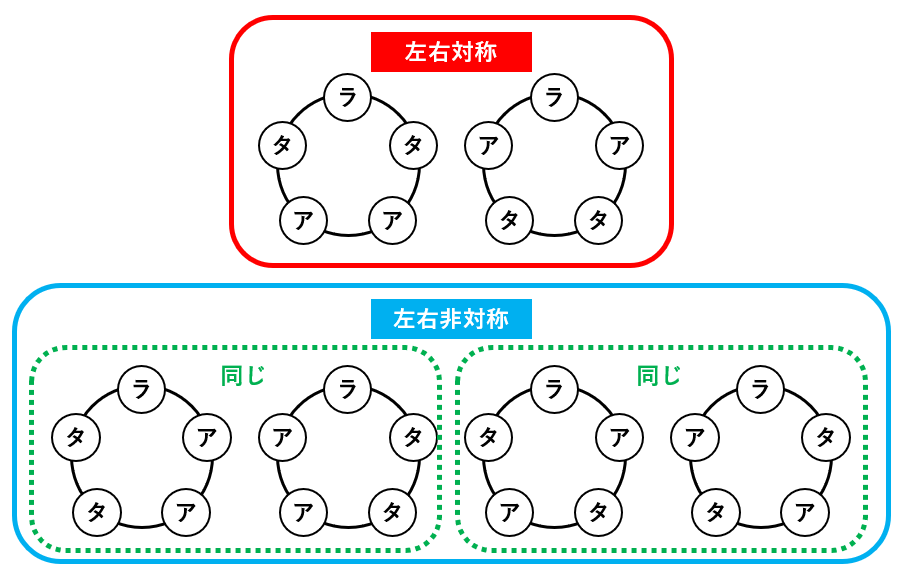
赤で囲った左右対称のつなぎ方は、すべて異なるつなぎ方で2通りです。一方、青で囲った左右非対称のつなぎ方は、2つずつ同じつなぎ方が出てくるので、4÷2=2(通り)です。したがって、(3)の答えは2+2=4(通り)です。
同じものを含む数珠順列の問題を計算で解くなら、左右非対称の並べ方を2で割り、左右対称の並べ方は割りません。計算する場合でも、ある程度は図を描かないと、正しい答えにたどり着けないでしょう。







コメント