トイレの花子さんは親友のいっちゃんと久しぶりに会いました。
いっちゃんは髪が伸びる市松人形です。花子さんのことを「はなちゃん」と呼んでいます。

はなちゃん、久しぶり!

しばらく会ってなかったけど、何してたの?

もっともっと髪を伸ばすための修行をしてたの。私、特級呪物になりたくってさ。

私は特級呪物になってテレビ出演して、たくさんの人たちを呪いころ……いえ、幸せにして、みんなからチヤホヤされるのが夢なの。ライバルはオカルトコレクター・田中俊行さんの相棒・チャーミーよ!

へぇ~。ところで、いっちゃん、修行は成功したの?

それが実は……。
平均とは何か?
【問題】市松人形のいっちゃんはもっともっと髪を伸ばすための修行をしました。
(1) 修行を始めてから5日間について、1日の髪の伸び方は下の表の通りでした。平均して髪は1日に何mm伸びましたか。
| 1日目 | 2日目 | 3日目 | 4日目 | 5日目 |
|---|---|---|---|---|
| 0.31mm | 0.25mm | 0.35mm | 0.28mm | 0.36mm |
(2) 修行を始めてから6日間について、1日の髪の伸び方の平均は0.32mmでした。6日目に髪は何mm伸びましたか。
(3) 修行の最終日に髪が0.41mm伸びました。1日の髪の伸び方の平均は、最終日の前日までの期間で0.28mmでしたが、最終日も含めると0.29mmになりました。いっちゃんは何日間修行をしましたか。また、修行を始めてから終えるまで、髪は何mm伸びましたか。
【問題】の中にある「平均」とは、いったい何なのでしょうか?
平均は「平(たいら)らに均(なら)す」という意味です。でこぼこをなくして平らにすることが平均です。
たとえば、4、5、6の平均を求めてみましょう。下の図からもわかる通り、4、5、6の平均は5です。
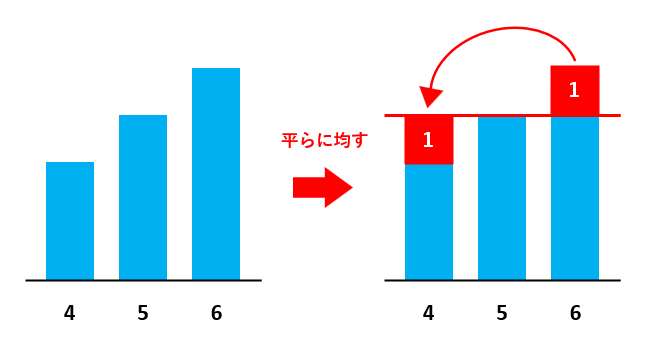
5より出っ張っている6と、5よりへこんでいる4を平らにするため、6から4へ1を移動しました。平均すると、出っ張っている部分とへこんでいる部分の数値(面積や体積など)は等しくなります。このことは、平均を面積図で考えるとき使います。
さて、どうすれば平均を計算で求められるのでしょうか?
4、5、6の平均を求めるとき、3つの数の合計は4+5+6=15なので、これを個数の3で割って15÷3=5です。つまり、「合計÷個数=平均」が成り立ちます。この式と、この式を変形した2つの式を合わせて「平均の公式」といわれることがあります。
- 合計÷個数=平均
- 合計÷平均=個数
- 平均×個数=合計
平均を求めるにはどうする?
(1)は平均を求めるだけなので、「合計÷個数=平均」を利用します。
5日間に伸びた髪の長さの合計は0.31+0.25+0.35+0.28+0.36=1.55です。したがって、平均は1.55÷5=0.31(mm)です。
仮平均を利用する
(1)は普通に合計を求めても、それほど計算が大変ではありません。しかし、仮平均を利用すると、もっと計算が楽になります。
仮平均とは、自分で好きに決めた平均のことです。仮平均はどんな数にしてもいいのですが、小学生は一番小さい数を仮平均にするのが楽でしょう。
(1)では仮平均を0.25にします。このとき、それぞれの数と仮平均の差が下の表です。
| 1日目 | 2日目 | 3日目 | 4日目 | 5日目 |
|---|---|---|---|---|
| 0.06mm | 0mm | 0.1mm | 0.03mm | 0.11mm |
これらの平均は(0.06+0+0.1+0.03+0.11)÷5=0.3÷5=0.06です。これを仮平均に加えて0.25+0.06=0.31(mm)が平均です。
仮平均と平均の関係は下の図の通りです。0.25よりも上の部分を平均したと考えましょう。
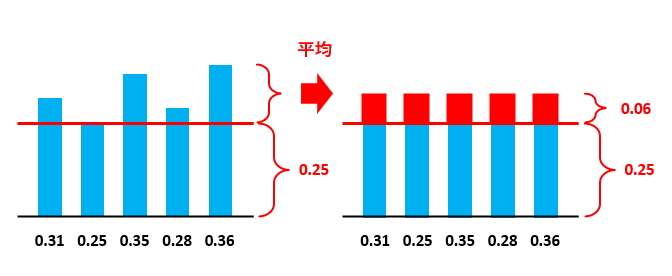

0.25を仮平均にすると、2日目の差が0になります。だからといって、2日目を無視して4日間とするのではなく、2日目も含めて5日間で計算しましょう。
合計の差から何がわかるの?
(2)は、6日間の平均がわかっているので、「平均×個数=合計」より、6日間の合計は0.32×6=1.92です。(1)より、5日間の合計は1.55です。合計の差は1.92-1.55=0.37で、これは6日目に伸びた髪の長さです。したがって、(2)の答えは0.37mmです。
平均で面積図をどう利用するの?
(3)では、平均はわかっていますが、個数(日数)も合計もわかっていません。このような場合は面積図を利用すると便利です。
面積図の縦を平均、横を個数(日数)にすると、面積は合計になります。(3)を面積図で表すと下の通りです。
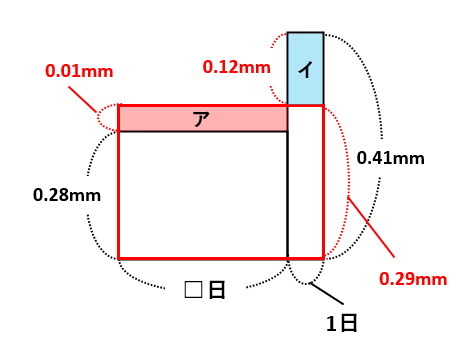
0.29mmより出っ張っているイを、0.29mmよりへこんでいるアに移動したと考えられるので、アの面積とイの面積は等しくなります。したがって、0.01×□=0.12×1より□=0.12÷0.01=12(日)です。
いっちゃんが修行した日数は、12日に最終日の1日を足した13日間です。また、修行を始めてから終えるまで、髪は0.29×13=3.77(mm)伸びました。
合計の差を利用する
(3)も、(2)と同じように、合計の差を利用することもできます。
いっちゃんが修行した日数のうち、最終日を除いた日数を□日とすると、0.29×(□+1)-0.28×□=0.41です。分配法則を使って( )を外すと、0.29×□+0.29-0.28×□=0.41なので、0.01×□=0.41-0.29=0.12となって□=0.12÷0.01=12(日)を求められました。
この後は面積図を利用した場合と同じで、いっちゃんが修行した日数は、12日に最終日の1日を足した13日間です。また、修行を始めてから終えるまで、髪は0.29×13=3.77(mm)伸びました。
人形の髪が伸びるのはなぜ?
髪が伸びる人形は怪談の定番です。そんな人形の中でも有名なのが市松人形でしょう。

市松人形
市松人形はおかっぱ頭の女の子が有名ですが、男の子の人形もあります。女児の遊び道具や裁縫の練習台として使われただけでなく、大人の男性の着せ替え人形遊びに使われたともいわれます。名前の由来は、江戸時代に大人気だった美形歌舞伎役者、佐野川市松(さのがわいちまつ)に似せて作られたからという説の他、諸説あります。
市松人形の髪が伸びる理由は科学的に説明されます。1つめの説明は、抜けた髪が途中で引っかかって、毛先が伸びたように見える、というものです。2つめの説明は、本物の人間の髪の毛を使った場合、その髪の毛は頭皮から抜けてもしばらくは伸びる、というものです。特に、毛根のついた髪の毛は、接着剤(にかわ)に含まれるコンドロイチンの育毛作用で伸びるともいわれます。もっとも、これらの理由だと、数ミリから数センチ伸びるだけだけです。
また、昔の市松人形は、実際に見える長さの2倍以上の髪の毛を植え込んで作られたため、接着剤が緩んだところは髪の毛が伸びたように見えます。これも超常現象ではありません。
一方、1970年代のオカルトブーム以降、「髪が伸びる人形」としてメディアにも登場してきたのは蔓念寺(北海道岩見沢市)のお菊人形です。お菊人形については、オカルト界の重鎮、並木伸一郎先生が現地取材をしています。詳細はYouTubeの「並木ミステリーCH」で確認してください。

せっかく修業したのに、髪の毛が5ミリも伸びなかったのよ。ほんと、やってらんないわ。

数ミリでも伸びればすごいんじゃない?

ううん、納得いかない! だから、私、はなちゃんと一緒に勉強して、良い学校に行って、科学的に髪を伸ばす方法を追求するわ!

えっ? そこはオカルトじゃなくて科学なんだ……。

令和の時代に必要なのは科学の知識と技術よ。私は理系に進んで、呪物で最初のリケジョになるのよ!






コメント