中学3年生の狸雄は、立方体を切断する問題が苦手で悩んでいました。そんな狸雄に声をかけてきたのが豆腐小僧です。
豆腐小僧は「包丁で切っても形の崩れない不思議な豆腐がありますよ。この豆腐を使って立方体の切断を勉強してみませんか?」と言います。狸雄は藁(わら)にも縋(すが)る思いで不思議な豆腐を買いました。
中学受験生や高校受験生は、狸雄と一緒に立方体の切断の基礎を学びましょう。
立方体を切断してできるのはどんな立体?
【問題】不思議な豆腐は、一辺の長さが6cmの立方体ABCD-EFGHです。この豆腐を(1)~(3)の3点を通る平面で切るとき、点Hを含む方の豆腐の体積は何cm3になりますか。
(1) 図1で、3点A、C、Fを通る平面で切ります。
(2) 図2で、IはBFの真ん中の点で、CJは4cmです。このとき、3点A、I、Jを通る平面で切ります。
(3) 図3で、KはADの真ん中の点です。このとき、3点C、F、Kを通る平面で切ります。
立方体の切断の問題では、立方体を切断してできる図形(切り口)がどのような形になるかを考える必要があります。このとき、次の2つのルールを利用します。
- 同じ面にある点を結ぶ。
- 向かい合う面の切り口は平行になる。
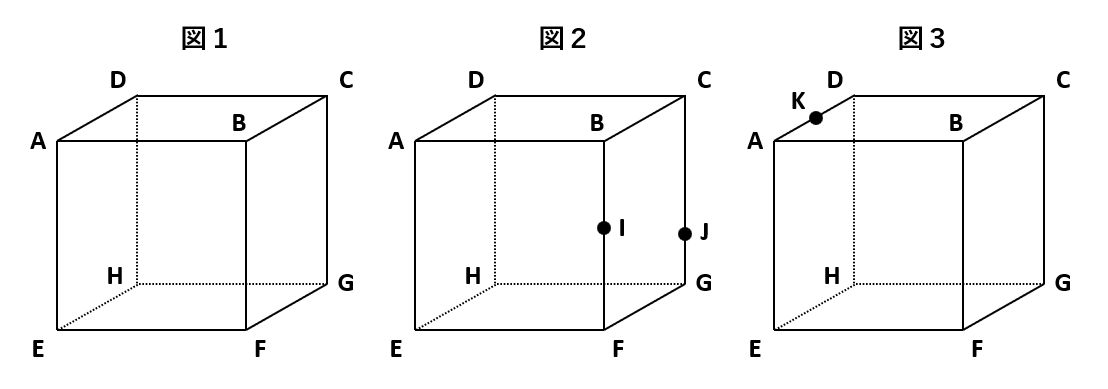
(1)は、ルール1を利用して、同じ面にあるAとC、CとF、FとAをそれぞれ結ぶと、下の図の左のようになります。(赤線が2点を結んだ線です)
点Hを含む方の豆腐の体積を求めるのは難しそうです。そこで、点Hを含まない方の豆腐の体積を求め、豆腐全体の体積から引くことにします。
上の図の右の立体(点Hを含まない方の豆腐)は三角錐C-ABFです。三角錐を含む錐体の体積は「底面積×高さ×\(\frac{1}{3}\)=錐体の体積」なので、三角形ABFを底面とすると、三角形ABFに垂直なBCが高さです。三角形ABFは、AB=BF、角ABFが垂直の直角二等辺三角形で、面積はAB×BF×\(\frac{1}{2}\)=6×6×\(\frac{1}{2}\)(cm2)です。また、BC=6(cm)です。
したがって、求める体積は(立方体ABCD-EFGHの体積)-(三角錐C-ABFの体積)=6×6×6-6×6×\(\frac{1}{2}\)×6×\(\frac{1}{3}\)=216-36=180(cm3)です。

三角錐の体積は、三角形BCFを底面とするならば高さはAB、三角形ABCを底面とするならば高さはBFだよ。AB=BC=BF=6(cm)だから、計算式は変わらないんだ。でも、三角形ACFを底面とすると、Bから三角形ACFに下ろした垂線が高さになるので、計算が面倒になる。立体の体積を求める場合、直角に注目して底面と高さを決めよう。
断頭四角柱の体積はどうやって求めるの?
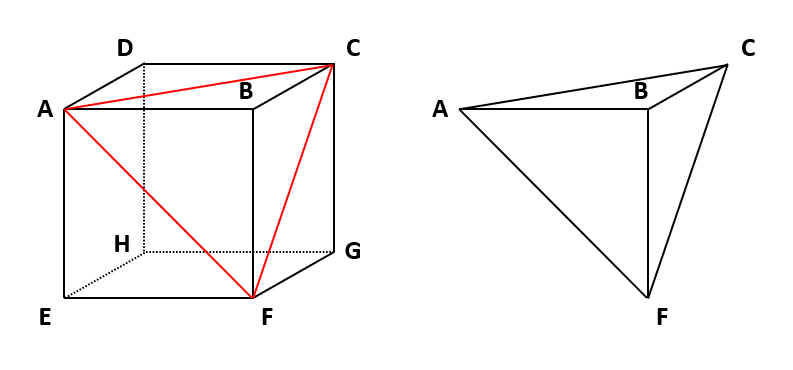
(2)も、ルール1を利用して、同じ面にあるAとI、IとJをそれぞれ結ぶと、下の図の左のようになります。(赤線が2点を結んだ線です)
さらに、ルール2を利用して、AIとIJに平行な線をそれぞれに向かい合う面に描くと、下の図の右のようになります。このとき、IJを斜辺(直角と向かい合う辺)とする直角三角形を描いて、この直角三角形を、一辺がADと重なるように平行移動します。そして、点LとA、Jを結ぶとわかりやすいでしょう。(平行四辺形AIJLが切断面です)
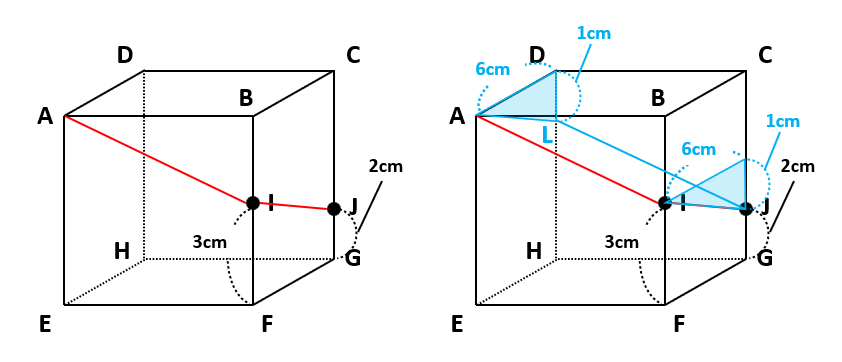
(2)のように、四角柱を斜めに切断して、切断面が平行四辺形になる立体は「断頭四角柱(だんとうしかくちゅう)」と呼ばれることがあります。断頭四角柱の体積を求める場合、この四角柱をひっくり返して、高さが等しくなるように180°回転させてくっつけます。
下の図では、左の断頭四角柱をひっくり返して180°回転させてくっつけたのが右の四角柱です。
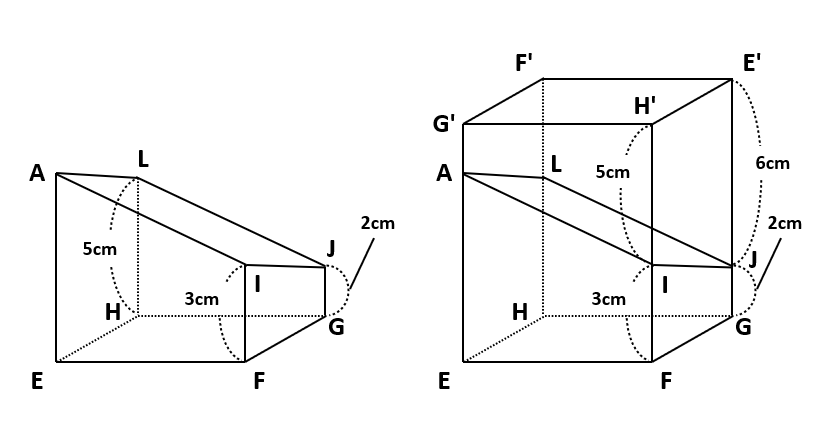
右の四角柱EFGH-G’H’E’F’の体積は「底面積×高さ=体積」より6×6×8なので、この体積を半分にして6×6×8÷2=144(cm3)です。

断頭四角柱の体積を無理やり公式化すれば、「底面積×高さの平均=断頭四角柱の体積」となるよ。ただし、「高さの平均=向かい合う辺の長さの和÷2」だ。たとえば、(2)の断頭四角柱は、IFと向かい合う辺はLHなので、平均の高さは(IF+LH)÷2=(3+5)÷2=4となって、体積は6×6×4=144(cm3)と求められるんだ。この考え方は、三角柱や円柱などの柱体でも使えるよ。
切断面が台形になる立体の体積はどうやって求めるの?
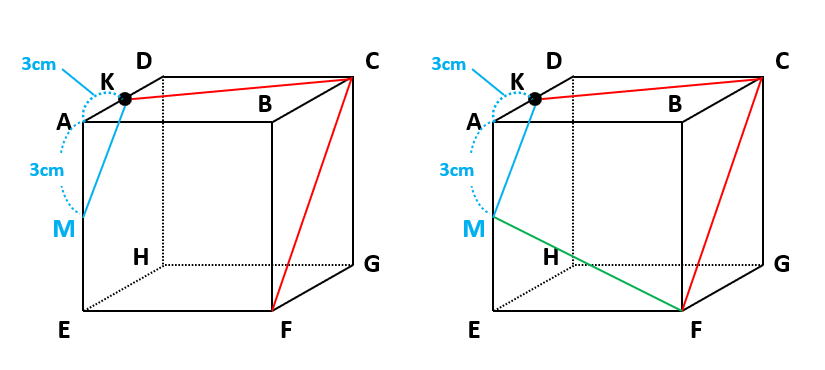
(3)もまずは、ルール1を利用して、同じ面にあるCとF、CとKをそれぞれ結ぶと、下の図の左のようになります。(赤線が2点を結んだ線です)
次に、ルール2を利用して、CFに平行な線KMを向かい合う面に描きます。このとき、BC=6(cm)、AK=3(cm)なので、下の図の左のように、三角形BCFと相似な三角形AKMができる位置をMにします。(青線がCFに平行な線のKMです)
最後に、ルール1を利用して、同じ面にあるMとFを結ぶと、下の図の右のようになります。(緑線が2点を結んだ線です)
切断面CFMKは台形なので、(2)のように断頭四角柱と同じ考え方はできません。そこで、向かい合う面の三角形BCFと三角形AKMが相似なので、BA、CK、FMをそれぞれ小さい三角形AKMの方に延長します。延長した直線が一点Nで交わり、下の図のように三角錐N-BCFになります。
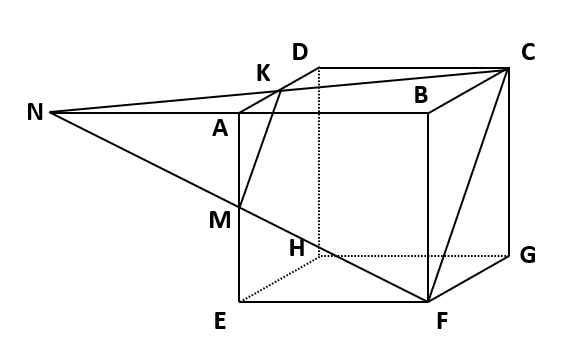
三角形BCFと三角形AKMが相似なので、三角錐N-BCFと三角錐N-AKMも相似です。三角形BCFと三角形AKMの相似比はBC:AK=6:3=2:1より、三角錐N-BCFと三角錐N-AKMの相似比も2:1です。したがって、NB:NA=2:1より、NA=AB=6(cm)を求められます。
三角錐N-BCFの体積は(三角形BCFの面積)×NB×\(\frac{1}{3}\)=6×6×\(\frac{1}{2}\)×12×\(\frac{1}{3}\)=72(cm3)で、三角錐N-AKMの体積は(三角形AKMの面積)×NA×\(\frac{1}{3}\)=3×3×\(\frac{1}{2}\)×6×\(\frac{1}{3}\)=9(cm3)です。これより、立体AKM-BCFの体積は(三角錐N-BCFの体積)-(三角錐N-AKMの体積)=72-9=63(cm3)です。
したがって、求める体積は(立方体ABCD-EFGHの体積)-(立体AKM-BCFの体積)=6×6×6-63=153(cm3)です。

立体AKM-BCFの体積は相似比を使って求めることもできるよ。三角錐N-BCFと三角錐N-AKMの相似比は2:1なので、体積比が(2×2×2):(1×1×1)=8:1だから、立体AKM-BCFの体積は(三角錐N-BCFの体積)×\(\frac{7}{8}\)=6×6×\(\frac{1}{2}\)×12×\(\frac{1}{3}\)×\(\frac{7}{8}\)=63(cm3)だね。




コメント