中学3年生の狸雄は、高校受験の勉強でたまったストレスを発散するため、いたずらを思いつきました。近所の空き地にミステリーサークルを作ることです。
そんな狸雄と一緒に、中学受験算数でよく出る円の面積の問題について考えてみましょう。三平方の定理を使った解き方も記載したので、中学数学の勉強にもなるはずです。

ミステリーサークル(画像はWikipediaより)
半径が分からない円の面積を求める方法は?
【問題】狸雄は、一辺が10mの正方形の空き地にミステリーサークルを作るため、円と正方形を組み合わせた下の図を描きました。ただし、円周率は3.14とします。
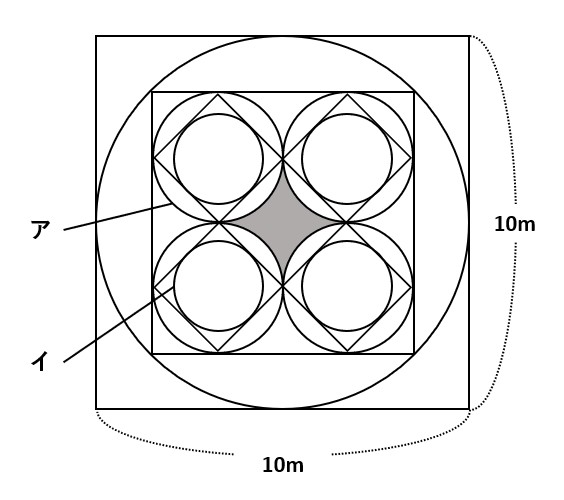
(1) アの円の面積は何m2ですか。
(2) イの円の面積は何m2ですか。
(3) 色のついた部分の面積は何m2ですか。
【問題】の図では、一番外側の正方形の一辺が10mであることしかわかっていません。このような場合、半径がわからない円の面積は、正方形の面積を利用して求めます。
(1)では、下の図のように、アの円の半径を□mとすると、内側の正方形の一辺の長さが(□×4)mと表せます。
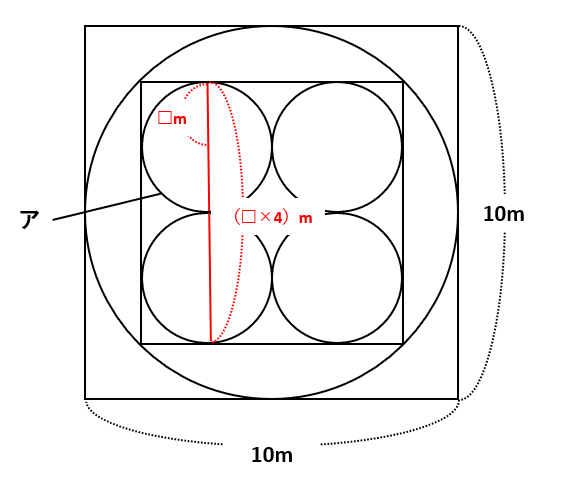
さらに、下の図のように、内側の正方形を回転させると、内側の正方形の対角線の長さが外側の正方形の一辺の長さと等しいことがわかります。
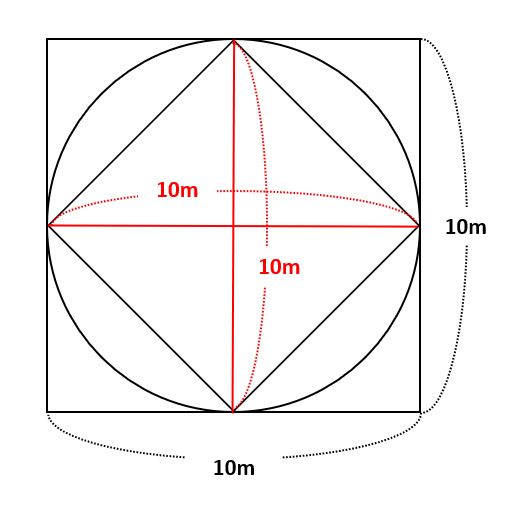
ここで正方形の面積を2つの式で表してみます。小学校でも習う式は「一辺×一辺=面積」です。一方、正方形はひし形の仲間なので「対角線×対角線÷2=面積」も成り立ちます。
内側の正方形の面積は、「一辺×一辺=面積」より(□×4)×(□×4)、「対角線×対角線÷2=面積」より10×10÷2=50(m2)です。したがって、(□×4)×(□×4)=50となり、□×□=50÷16=\(\frac{50}{16}\)=\(\frac{25}{8}\)です。
アの円の面積は□×□×3.14=\(\frac{25}{8}\)×3.14=9.8125(m2)です。

中学3年生は、□×□の値を求めるという回りくどいことをしないで、三平方の定理を使って□×4=5\(\sqrt{2}\)より□=\(\frac{5}{4}\sqrt{2}\)を求められる。円周率も3.14じゃなくて\(\pi\)を使って、アの円の面積は\({(\frac{5}{4}\sqrt{2})}^2\times\pi\)=\(\frac{25}{8}\pi\)(m2)だよ。
(2)では、まずイの円を囲む正方形の一辺の長さを求めます。
下の図で、イの円を囲む正方形(赤で囲った正方形)の面積は、「対角線×対角線÷2=面積」より(□×2)×(□×2)÷2=\(\frac{25}{8}\)×4÷2=\(\frac{25}{4}\)(m2)です。この正方形の一辺の長さを△mとすると、「一辺×一辺=面積」より△×△=\(\frac{25}{4}\)なので△=\(\frac{5}{2}\)(m)です。
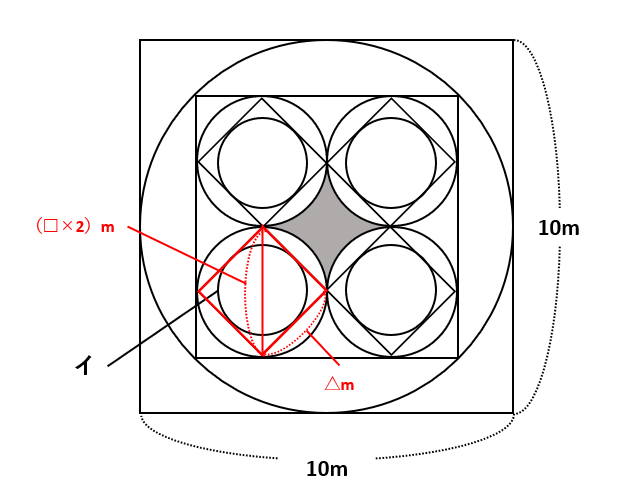
イの円の半径は\(\frac{5}{2}\)÷2=\(\frac{5}{4}\)(m)より、イの円の面積は\(\frac{5}{4}\)×\(\frac{5}{4}\)×3.14=4.90625(m2)です。

△=\(\frac{5}{4}\sqrt{2}\times\frac{1}{\sqrt{2}}\)=\(\frac{5}{4}\)なので、イの円の面積は\({(\frac{5}{4})}^2\times\pi\)=\(\frac{25}{16}\pi\)(m2)と求めることもできるね。
変な形の図形の面積を求めるには?
(3)のような変な形の図形の面積を求める場合、簡単に面積を求められる図形同士を引き算します。(3)では、次のような引き算を考えるといいでしょう。
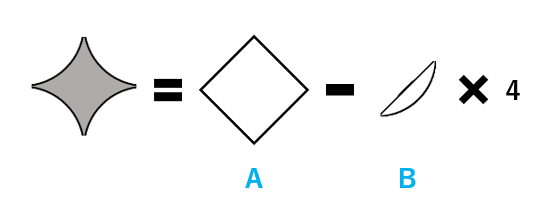
Aの正方形の面積は、(2)より\(\frac{25}{4}\)m2です。(Bの図形)×4の面積は、アの円の面積からAの正方形の面積を引けば求められるので、\(\frac{25}{8}\)×3.14-\(\frac{25}{4}\)=\(\frac{25}{4}\)×(1.57-1)=\(\frac{25}{4}\)×0.57(m2)です。
したがって、(3)の答えは、\(\frac{25}{4}\)-\(\frac{25}{4}\)×0.57=\(\frac{25}{4}\)×(1-0.57)=2.6875(m2)です。

Aの正方形の面積は\(\frac{25}{4}\)m2で、(Bの図形)×4の面積は\(\frac{25}{8}\pi\)-\(\frac{25}{4}\)(m2)なので、(3)の答えは\(\frac{25}{4}\)-\(\{\frac{25}{8}\pi-\frac{25}{4}\}\)=\(\frac{25}{2}\)-\(\frac{25}{8}\pi\)=\(\frac{25}{8}(4-\pi)\)(m2)だね。
ミステリーサークルとは何だったのか?
ミステリーサークルは、田畑の穀物が円形に倒され、直径数十メートルの幾何学模様が現れる現象です。1980年代にイギリスを中心として報告され、世界的に話題となりました。当初は、宇宙人やUFOを原因とする説が有力で、霊や魔術などとの関連も主張されました。一方、プラズマや竜巻などの自然現象を原因とする科学的な説も唱えられました。
しかし、1991年、ミステリーサークルは人為的に作られたものであると判明しました。イギリスのダグ・バウワーとデイブ・チョーリーの老人2人組が簡単な道具と人力でミステリーサークルを作れることを実証したからです。これがきっかけで2人は1992年、「人々を笑わせ、そして考えさせる業績」に対して贈られるイグノーベル賞の物理学賞を受賞しました。
現在、多くの人々は「ミステリーサークルは超常現象ではない」と考えます。「サークルメーカー」と呼ばれる、ミステリーサークルを作る人々も堂々と情報発信しています。しかし、webムーの記事でも紹介されている通り、すべてのミステリーサークルが人為的に作られたとは限りません。ニセモノの中に本物がまぎれている可能性もあるのです。




コメント