高校2年生の舞理(まいり)は、同じ高校の3年生の霧斗(きりと)先輩が大好きです。大好き過ぎてストーカーしているほど……。そんな舞理が何やら企んでいます。

先日オカルトショップでイモリの黒焼きを買ったわ。これを粉にしてコーヒーに溶かせば、オリジナル惚れ薬になる。これを霧斗先輩に飲ませれば……。霧斗先輩はあたしのものよ。フフフ……。
そもそもイモリの黒焼きの粉がコーヒーに溶けるのかどうかは不明ですが、とりあえず溶けるということにして、濃度(濃さ)について解説します。
「濃度とは何か?」を理解しよう
【問題】高校2年生の舞理は、イモリの黒焼きの粉をコーヒーに溶かして惚れ薬を作ります。
(1) 100gのコーヒーに25gのイモリの黒焼きの粉を溶かすと何%の惚れ薬ができますか。
(2) 14%の惚れ薬250gにはイモリの黒焼きの粉は何g溶けていますか。
(3) 13%の惚れ薬200gと18%の惚れ薬300gを混ぜ合わせると何%の惚れ薬ができますか。
【問題】を解く前に、「%で表される濃度(濃さ)とはいったい何なのか?」を考えましょう。
溶質・溶媒・溶液とは何か?
中学受験算数でおなじみの食塩水を例に、理科でも使う言葉を解説します。
食塩水(塩水)とは、水に食塩を溶かした液体です。このような液体で、溶けている物質を「溶質」、溶質を溶かす液体を「溶媒(ようばい)」、溶質を溶液に溶かした液体を「溶液」といいます。中でも、溶媒が水の溶液を「水溶液」といいます。
食塩水の場合、溶質は食塩で、溶媒が水で、溶液が食塩水です。食塩の正式な名前が塩化ナトリウムなので、食塩水を「塩化ナトリウム水溶液」ともいいます。
濃度(濃さ)とは何か?
濃度(濃さ)とは、溶液の重さ(質量)に対する溶質の重さ(質量)の割合です。もっとわかりやすく言いかえると、「溶液の重さを100%にしたとき、溶質の重さは何%になるか?」です。「溶液の重さ=もとにする量」とわかれば、普通の割合と同じ方法で計算できます。(割合に不安がある読者は以下の記事で確認してください)

たとえば、150gの食塩水(溶液)に18gの食塩(溶質)が溶けているなら、「比べられる量÷もとにする量=割合」より18÷150=0.12で、0.12を100倍して12%です。
これを線分図で表すと次の通りです。食塩水の重さ150gを100%にしましょう。
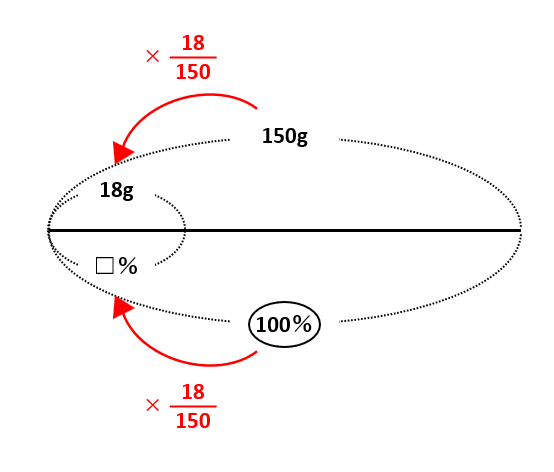
線分図の上の数字(重さ)に注目して、150gを18gにしたければ、150を\(\frac{18}{150}\)倍します。同じように100%も\(\frac{18}{150}\)倍すれば□%を求められるので、□=\(\frac{18}{150}\)×100=12(%)です。\(\frac{18}{150}\)×100が次の濃度の公式になっているのもわかるでしょう。
この公式を変形したのが次の式です。無理に覚える必要はなく、必要に応じてその場で導けるようにしましょう。
- 溶液の重さ×\(\frac{濃度(%)}{100}\)=溶質の重さ
- 溶質の重さ÷濃度(%)×100=溶液の重さ
濃度の基本問題を解こう
【問題】も食塩水と同じように考えると、溶質がイモリの黒焼きの粉で、溶媒がコーヒーで、溶液が惚れ薬です。
惚れ薬の濃度を求めよう
(1)は、「惚れ薬(溶液)の重さ=イモリの黒焼きの粉(溶質)の重さ+コーヒー(溶媒)の重さ」に要注意です。
濃度の公式にあてはめれば、「\(\frac{イモリの黒焼きの粉の重さ}{惚れ薬の重さ}\)×100=濃度(%)」より\(\frac{25}{25+100}\)×100=20(%)が答えです。
線分図は次の通りです。
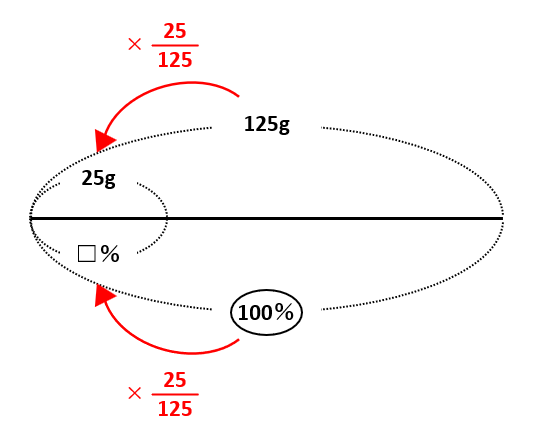
線分図の上の数字(重さ)に注目して、125gを25gにしたければ、125を\(\frac{25}{125}\)倍します。同じように100%も\(\frac{25}{125}\)倍すれば□%を求められるので、□=\(\frac{25}{125}\)×100=20(%)です。
イモリの黒焼きの粉の重さを求めよう
(2)は、「溶液の重さ×\(\frac{濃度(%)}{100}\)=溶質の重さ」にあてはめれば、「惚れ薬の重さ×\(\frac{濃度(%)}{100}\)=イモリの黒焼きの粉の重さ」より250×\(\frac{14}{100}\)=35(g)が答えです。
線分図は次の通りです。
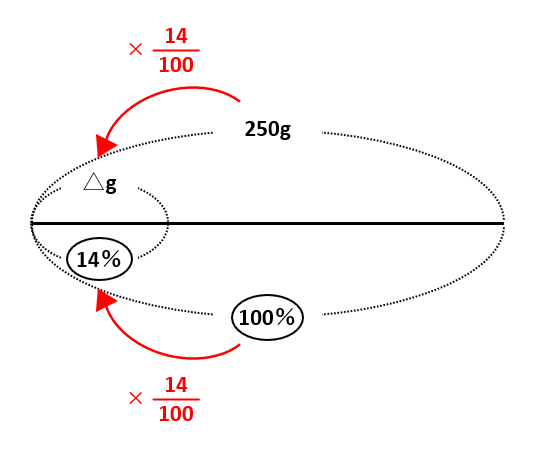
線分図の下の数字(濃度)に注目して、100%を14%にしたければ、100を\(\frac{14}{100}\)倍します。同じように250gも\(\frac{14}{100}\)倍すれば△gを求められるので、△=250×\(\frac{14}{100}\)=35(g)です。
混ぜ合わせの問題を解こう
(3)は、入試でよく出る混ぜ合わせの問題です。濃度の意味を理解していれば、何も難しくはありません。
まず、13%の惚れ薬200gと18%の惚れ薬300gに溶けているイモリの黒焼きの粉の重さをそれぞれ求めます。
- 13%の惚れ薬200g … 200×\(\frac{13}{100}\)=26(g)
- 18%の惚れ薬300g … 300×\(\frac{18}{100}\)=54(g)
次に、混ぜ合わせた後の惚れ薬について考えます。イモリの黒焼きの粉の重さは合計26+54=80(g)で、惚れ薬の重さは合計200+300=500(g)です。
したがって、混ぜ合わせた後の惚れ薬の濃度は\(\frac{80}{500}\)×100=16(%)です。
混ぜ合わせの問題を面積図で解こう
面積図や比が大好きな受験生のために別解も紹介します。
「溶液の重さ×\(\frac{濃度(%)}{100}\)=溶質の重さ」が成り立つので、濃度の問題では、溶液の重さを横、濃度を縦、溶質の重さを面積とした面積図を使えます。この面積図では、濃度を小数に直さずに%のまま使って構いません。
(3)の面積図を描くと次の通りです。
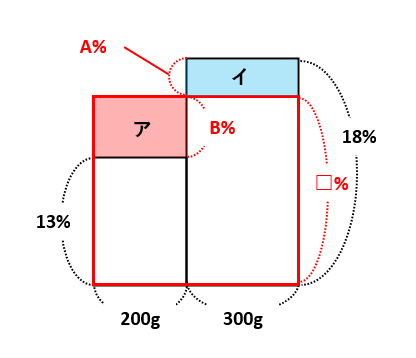
混ぜ合わせると、13%の惚れ薬と18%の惚れ薬の濃度が平均されます。そのため、上の面積図のアの面積とイの面積は等しくなります。「アの面積=イの面積」から200×B=300×Aとなり、A:B=300:200=3:2です。
A+B=18-13=5(%)なので、B=5×\(\frac{3}{3+2}\)=3(%)です。したがって、□=13+3=16(%)が(3)の答えです。
混ぜ合わせの問題を天秤図で解こう
面積図の「アの面積=イの面積」から、A%とB%は2種類の惚れ薬の重さの逆比になっていることがわかります。このことを理科の天秤(てこ)として表したのが次の天秤図です。
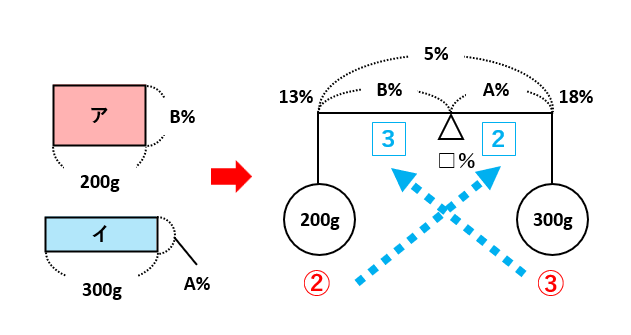
惚れ薬の重さをおもりで、惚れ薬の濃度をおもりから支点までの腕の長さで表します。腕の左端は一番低い濃度の惚れ薬に、右端は一番高い濃度の惚れ薬にします。中央の支点は、これらを混ぜ合わせた後の濃度です。
天秤図からA:B=2:3なので、B=5×\(\frac{3}{3+2}\)=3(%)となり、□=13+3=16(%)が(3)の答えです。

濃度の意味がわかってれば、わざわざ面積図や天秤図を使う必要もないんじゃないかしら? 普通に溶質の重さを求めるだけで解けるし、この解き方の方が中学数学の方程式にもつながると思うんだけど……。中学受験算数はよくわからない世界だわ。
イモリの黒焼きとは何なのか?
中学受験生はイモリとヤモリの違いを覚えましょう。イモリは両生類で、ヤモリは爬虫類です。

イモリの黒焼き
イモリは漢字で「井守」と書き、地下水をくみ上げるための井戸を守っているから、体が水で湿っている両生類です。一方、ヤモリは漢字で「家守」と書き、地上にある家を守っているから、体が乾燥している爬虫類です。イモリは黒い体に赤い腹で、ヤモリは全身が鱗で覆われています。
イモリの黒焼きが惚れ薬として流通したのは江戸時代です。オスのイモリの黒焼きを自分にふりかけ、メスのイモリの黒焼きを好きな相手にふりかることで、お互いに惹かれ合うといわれていました。
もともとは中国の漢の時代、武帝が宮女たちの浮気を防止するため、宮女たちの体にヤモリの黒焼きを塗ったといわれます。日本ではヤモリとイモリが混同されたようです。
宮崎駿監督のアニメーション映画『千と千尋の神隠し』では、イモリの黒焼きが食べ物として登場します。このことからもわかる通り、イモリの黒焼きは、ふりかけたり体に塗ったりするだけでなく、食べようと思えば食べられます。現在も、精力増強や滋養強壮に効果のある漢方薬として販売されています。

霧斗先輩、あたしが心を込めてコーヒーを淹れました。どうぞ召し上がってください。

舞理ちゃんの気持ちは嬉しいけど、僕はコーヒーが苦手で飲めないんだ。ごめんね。

そ、そんな……。





コメント